algébriquement

algébriquement

algébrique [ alʒebrik ] adj.
• XVIIIe; algébraïque 1585; de algèbre
♦ Relatif à l'algèbre, qui s'effectue par l'algèbre. Calcul numérique et calcul algébrique. — Mesure, quantité algébrique. Courbe, équation, fonction algébrique. Nombre algébrique. Topologie algébrique. — Adv. ALGÉBRIQUEMENT , 1782 .

● algébriquement adverbe Suivant les règles de l'algèbre. ● algébriquement (expressions) adverbe Corps algébriquement clos, corps commutatif K tel que tout polynôme à coefficients dans K a une racine dans K.

⇒ALGÉBRIQUEMENT, adv.
Selon les méthodes et les règles de l'algèbre :
• 1. ... les polynômes [de cette succession] (...) caractérisent algébriquement deux accords parfaits majeurs ...
C. DURUTTE, Esthétique musicale, Résumé élémentaire de la technie harmonique, 1876, p. 367.
• 2. Toute reconstruction du monde (tout ou partie) est imparfaite ou incomplète. Comment espérer qu'un petit échafaudage philosophique pourra représenter même algébriquement le monde.
J. RIVIÈRE, ALAIN-FOURNIER, Correspondance, lettre de J. R. à A.-F., nov. 1906, p. 330.
• 3. Ceux qui ont lu quelque exposition du système d'Einstein, soit traduite de l'inventeur lui-même, soit transposée par quelque géomètre compétent, ont pu remarquer deux choses, l'extrême difficulté des formules et des conceptions qui y sont supposées, et l'extrême faiblesse des commentaires de langue vulgaire. Algébriquement tout est correct; humainement tout est puéril.
ALAIN, Propos, 1922, p. 398.
Prononc. :[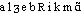]. Pour la transcription par [] ouvert de LITTRÉ, cf. algébrique.
Étymol. ET HIST. — 1782 « conformément à l'algèbre » (LINGUET, Annales politiques, civiles et litt., t. 13, p. 213, d'apr. GOHIN 1903, p. 251).
Dér. de algébrique; suff. -ment2.
STAT. — Fréq. abs. litt. :4.
BBG. — BÉL. 1957. — PAMART (P.). Lorsque le bon usage cesse d'être académique. Vie Lang. 1963, n° 137, p. 427.

algébriquement [alʒebʀikmɑ̃] adv.
ÉTYM. 1782; de algébrique.
❖
1 Par l'algèbre; d'une manière algébrique. || Notion formulée algébriquement. — (Au sens de l'algèbre moderne). || Corps commutatif algébriquement clos.
2 Rare. || Raisonner algébriquement, avec rigueur. ⇒ Mathématiquement.

Encyclopédie Universelle. 2012.

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • ALGÉBRIQUEMENT — adv. Conformément à l’algèbre …   Dictionnaire de l'Academie Francaise, 8eme edition (1935)

  • algébriquement — (al jè bri ke man) adv. D une manière algébrique, selon les règles de l algèbre. ÉTYMOLOGIE    Algébrique et ment …   Dictionnaire de la Langue Française d'Émile Littré

  • Champ Algébriquement Fermé — Corps algébriquement clos En mathématiques, un corps K est dit algébriquement clos si tout polynôme de degré supérieur ou égal à un, à coefficients dans K, admet (au moins) une racine dans K. Dans ce cas, chacun de ces polynômes se divise en… …   Wikipédia en Français

  • Champ algébriquement fermé — Corps algébriquement clos En mathématiques, un corps K est dit algébriquement clos si tout polynôme de degré supérieur ou égal à un, à coefficients dans K, admet (au moins) une racine dans K. Dans ce cas, chacun de ces polynômes se divise en… …   Wikipédia en Français

  • Corps Algébriquement Clos — En mathématiques, un corps K est dit algébriquement clos si tout polynôme de degré supérieur ou égal à un, à coefficients dans K, admet (au moins) une racine dans K. Dans ce cas, chacun de ces polynômes se divise en facteurs linéaires. Il peut… …   Wikipédia en Français

  • Corps algebriquement clos — Corps algébriquement clos En mathématiques, un corps K est dit algébriquement clos si tout polynôme de degré supérieur ou égal à un, à coefficients dans K, admet (au moins) une racine dans K. Dans ce cas, chacun de ces polynômes se divise en… …   Wikipédia en Français

  • Corps algébriquement clos — En mathématiques, un corps commutatif K est dit algébriquement clos si tout polynôme de degré supérieur ou égal à un, à coefficients dans K, admet (au moins) une racine dans K. Autrement dit, c est un corps qui n a pas d extension algébrique… …   Wikipédia en Français

  • Corps algébriquement clos — ● Corps algébriquement clos corps commutatif K tel que tout polynôme à coefficients dans K a une racine dans K …   Encyclopédie Universelle

  • CORPS (mathématiques) — La structure de corps n’est en fait qu’un cas particulier de la structure plus générale d’anneau [cf. ANNEAUX ET ALGÈBRES]; en plus des axiomes généraux, on stipule que le groupe multiplicatif des éléments inversibles est le complémentaire de 0.… …   Encyclopédie Universelle

  • GÉOMÉTRIE ALGÉBRIQUE — Sous sa forme actuelle, la géométrie algébrique est une branche de l’algèbre relativement récente (cf. ALGÈBRE, DEDEKIND). Pour «comprendre» les phénomènes d’intersection des courbes et des surfaces, il s’est révélé nécessaire d’élaborer des… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”